Directed Acyclic Graphs
A Directed Acyclic Graph (DAG) is a directed graph with no directed cycles.
This means that it is not possible to start from a vertex and come back to it by traversing the edges.
Remember that in a directed graph, edges can only be traversed in the direction of the arrow.
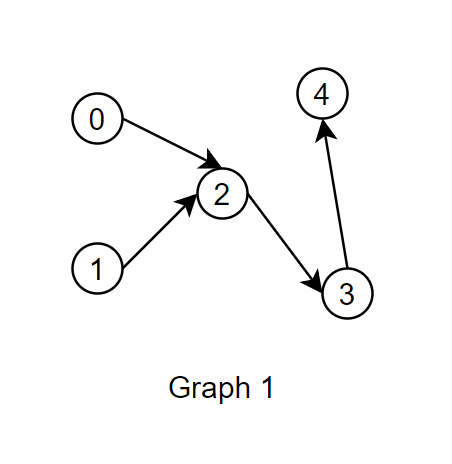
Graph 1 shows a DAG.
DAGs can be used to model many things. One common example is class scheduling, where certain classes may have prerequisites that must be completed first.
Note that we cannot have any cycles in these prerequisites. For example, Class A may have a prerequisite of Class B, and class B may have a prerequisite of Class C, but Class C cannot have a prerequisite of Class A.
This would mean that all 3 classes cannot be taken by anybody.
With DAGs, it is always possible to find a topological sort.
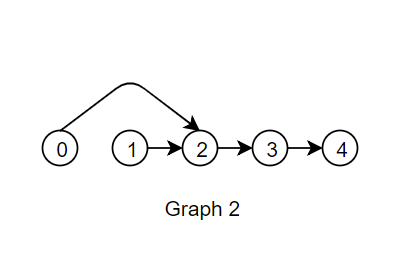
A topological sort gives an ordering of the nodes such that all edges point in only 1 direction. Graph 2 shows a topological sort for Pic4.
Note that there may be multiple topological sort for a DAG.
Tarjan’s algorithm for topological sort Tarjan’s algorithm gives us an O(V+E) method for topological sort. It is extremely similar to recursive DFS/BFS. In this case, we will use DFS to implement Tarjan’s algorithm.
Here is Java source code for Tarjan’s algorithm:
Stack<Node> stack = new Stack<Node>();
for(Node node : ListOfNodes){
if(node.visited == false){
dfs(node);
}
}
public void dfs(Node node) {
node.visited = true;
for(Node n : node.neighbors) {
if(n.visited == false) {
sort(n);
}
}
stack.push(node);
}
Afterwards, to get the topological sort, we reverse the order of the nodes in the stack
Justification:
Suppose we are currently considering an edge from Node v to Node w. There are 3 possible cases that might occur:
- dfs(w) has already been called and returned. Thus, w will be after v in the sort, since w is pushed into the stack first (remember that the stack gives the reverse topological order). This fulfills the requirement that w must come after v.
- dfs(w) has not yet been called. This means that w is an unexplored node, so we will call dfs(w). From the algorithm, it is clear that dfs(w) must be completed before v is pushed into the stack, so w will be pushed into the stack first. This fulfills the requirement that w must come after v.
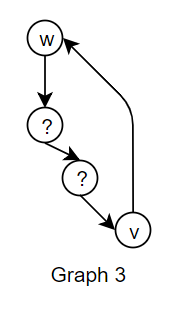
- dfs(w) has been called, but not yet returned. This means that there is a path from w to v (otherwise, dfs(v) would not have been called at this point). However, we also know that there is a path from v to w, since we are considering the edge v -> w. This forms a cycle, which cannot exist in a DAG. Thus, this case will never occur in a DAG. Graph 3 shows an example of this case.