DFS/BFS
We will now explore 2 fundamental algorithms for processing graphs: Depth-First Search (DFS) and Breadth-First Search (BFS). These algorithms are used in a wide variety of problems.
DFS is an algorithm used for traversing graphs. DFS begins at the root (in this case, an arbitrary node). After visiting a node, we will mark it to signal that we have already been to this node. Then, we will place the node’s non-visited neighbors on a stack. We then pop a node off the stack and repeat the process until the stack is empty.
stack.push(root);
while(!stack.isEmpty()){
Node current = stack.pop();
current.marked = true;
for(Node n : current.neighbors()){
if(n.marked == false){
stack.push(n);
}
}
}
BFS is very similar to DFS. In most cases, they are interchangeable. The only difference is that we use a queue instead of a stack.
queue.push(root);
while(!queue.isEmpty()){
Node current = queue.pop();
current.marked = true;
for(Node n : current.neighbors()){
if(n.marked == false){
queue.push(n);
}
}
}
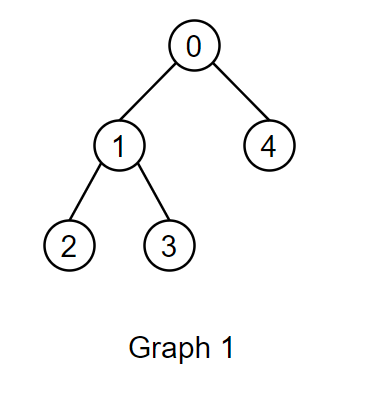
Let’s take a look at how DFS/BFS would explore the following graph.
DFS will explore as deep as it can along the graph. For example, DFS could explore Pic2 in the following order: 0-1-2-3-4. Notice how the algorithm explores along one branch of the graph until it can no longer continue. Then, it backtracks and explores the next branch, and repeats until all nodes have been visited.
BFS will explore each layer before moving on to the next layer. For example, in Pic2, BFS could explore in the following order: 0-1-4-2-3.