DFS/BFS applications
Bipartite check:
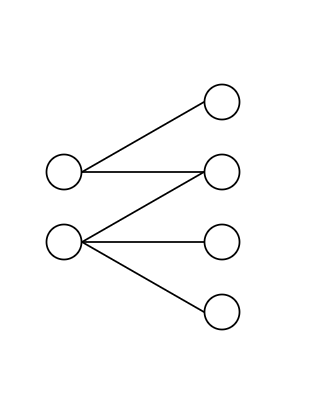
A graph is considered bipartite if we can divide the graph into 2 groups of nodes, with the special characteristic that all edges are between the groups of nodes.
The following graph shows an example of a bipartite graph:
Using the definition of a bipartite graph, we can come up with a way to check if a given graph is bipartite.
We traverse through the graph using either BFS/DFS. As we traverse the graph, we will color each node either red or blue, thus splitting the graph into a group of red nodes and a group of blue nodes.
We can assign the root node an arbitrary color, then run DFS/BFS. Suppose we are currently visiting a blue colored node. Then we can color all the node’s uncolored neighbors red. If the node has any colored neighbors, they must be blue. If we find any neighbors that are colored blue, then the graph is not bipartite.
Connected components:
We can also use BFS/DFS to identify the connected components of a graph.
We go through a list of all the nodes in the graph. Whenever we encounter an unmarked node, we will run BFS/DFS using that node as a root. During the traversal of the graph, we mark each node that we come across. When BFS/DFS stops, we have traversed a connected component. Then, we continue iterating through the list of nodes until every node has been marked.
Flood Fill:
Flood Fill is a simple algorithm that determines the total area connected to a node. This is the algorithm behind the bucket function in paint applications.
Flood Fill is extremely similar to DFS/BFS. The only difference is that we only add nodes of a certain color to the stack/queue, instead of all neighbors, as in DFS/BFS. We can also keep a counter to count how many nodes we covered.
We leave generating the source code as an exercise to the reader.
Hint: Start with either BFS/DFS, then modify it.