Graph Introduction
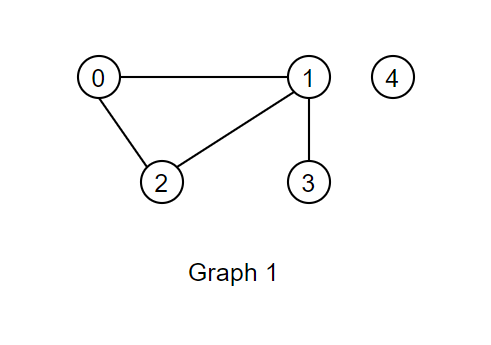
A graph is a collection of vertices (nodes) that are connected with a set of edges. The graph below has 4 nodes and 4 edges.
Graphs are used to model a vast variety of things, such as the spread of disease and computer networks. As graph theory (the study of graphs) is far too large of a subject cover, we will primarily focus on computer science algorithms concerning graphs.
We’ll need some basic definitions to begin:
Degree: the degree of a node is the number edges connected to that node. In Graph 1, Node 0 has a degree of 2.
Undirected graph: a graph containing undirected edges, which can be traversed in both directions. Undirected edges are typically represented with a straight line. Graph 1 shows an undirected graph.
Directed graph: a graph containing directed edges, which can only be traversed in one direction. Directed edges are typically represented with an arrow.
Path: There exists a path between two nodes if we can start from one node and traverse edges to get to the other node. For example, a path exists between Node 0 and Node 3 in Graph 1.
Cycle: A path is called a cycle if it begins and ends at the same node.
Connected graph: A graph is considered to be connected if we can find a path between every pair of vertices. The Graph 1 is not a connected graph, since we can’t reach Node 4 from some of the other nodes.
Tree: A connected graph with no cycles
Connected component: A connected component of a graph is a subset of its nodes such that these nodes are all connected with each other. For example, in Graph 1, a connected component would be Node 4 by itself, or Nodes 0,1,2, and 3.
There are 2 common methods to represent a graph in computer science:
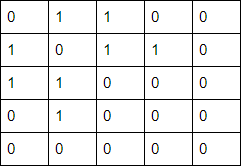
Adjacency Matrix: We create a square matrix with entries that tell us whether 2 nodes have an edge between them or not. For example, the adjacency matrix representing Graph 1 is shown below:
In order to determine if Node 0 and Node 2 are connected with an edge, we will look at entry (0,2) or (2,0). We see that it is a 1, so this means that Node 0 and Node 2 have an edge between them.
Adjacency List: For each node, we keep a list of nodes that are connected to that node.
For example, the adjacency list for Node 0 is {1,2}, as Node 0 is connected to Nodes 1 and 2.
The Adjacency List representation is usually more efficient than the Adjacency Matrix in sparse graphs (graphs with relatively few edges). As such, we will primarily use adjacency lists.