Hash Table
Introduction
Hash Table is a data structure that is extremely efficient at storing and retrieving values.
A hash table achieves O(1) time for retrieval of a value, in comaprison to O(N) for unsorted array.
Hash Function
Hash Tables rely on hash functions. Hash functions are mathematical functions that should display certain properties:
- If two objects, x and y, are considered to be equal, then hashFunction(x) must equal hashFunction(y)
- If two objects, x and y, are not equal, then hashFunction(x) should not equal hashFunction(y). This condition is not absolutely necessary, but should be met as much as possible.
- Hash functions should have their outputs be randomly distributed around their range.
- Hash functions should not be computationally expensive.
The value hashFunction(x) is x’s hash code.
Hash functions typically produce 32-bit integers as output.
Because there are infinite objects that could potentially be created, in comparison to the hash function’s limited range, it is inevitable that 2 distinct objects will have the same hash code. This is known as a collision.
In addition, the hash code for an object may not be immediately usable. For example, hash tables use an internal array to store information. This means that negative values and values over the array’s capacity are unusable.
We use a compression function to compress the hash codes into the proper range. A very simple example is to use modulus.
It is also possible that two different hash codes are compressed to the same number. This is also known as a collision.
Compression functions should ideally minimize collisions for a set of hash codes.
Collision Handling
Because collisions are guarenteed to occur, we need to be able to handle them.
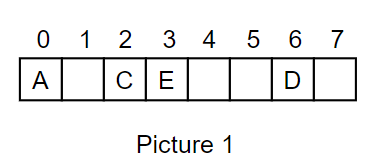
There are 2 main types of collision handling schemes. We’ll use Picture 1 and the following example:
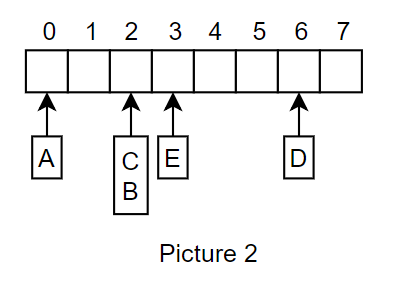
Suppose we are storing letters in our hash table. The client wants to insert the letter B. Let’s assume that B is hashed/compressed to location 2. We want to insert B into position 2, but letter C is already there.
-
Linear Probing: We will simply insert B into slot number (2 + 1) % (size of table) = 3 % 8 = 3. In this case, location 3 is also occupied, so we will go to location 4 and place B there. Later on, if we want to retrieve B again, we start at position 2 and continue traversing until B is found.
One problem with linear probing is that entries in the hash table tend to clump up. This makes our retrieval process expensive; we might have to traverse a significant part of the entire hash table until we find what we are looking for. Many different solutions have been created. For example, quadratic probing uses the sequence {1, 4, 9, 16, 25 …} as the distances between probes. In our example, we would probe position 2, position 2 + 1 = 3, then position 3 + 4 = 7. -
Separate Chaining: Another simple solution is to have each entry in the array be a data structure storing entries that hash to that location. In our example, we would simply place B inside the list stored at location 2, resulting in the following:
When we need to retrieve B, we simply go to position 2 and do a complete search of the list at location 2. We need to keep the list sizes relatively small so that lookup is quick. The value n/N = \lambda, where n is the number of elements in the hash table and N is the size of the table, is known as the load factor. Through experiments, it has been determined that the load factor should remain under 0.9 for good performance.
Once the load factor reaches the maximum value, a process known as rehashing occurs. The table size is expanded, and all elements in the table are reinserted. The process should ideally spread the elements across the table evenly.
Performance
The performance of a hash table is O(1) for insertion, deletion, and retrieval, making it extremely fast and useful when large amounts of data need to be stored and retrieved.
However, hash tables are vunerable to a denial-of-service attack. Because hash functions are deterministic (always returning the same output if the input is the same), an attacker can create large quantities of entries that all hash to the same output. This causes the performance of insertion, deletion, and retrieval to degrade to O(n), causing a server to do far more work than expected.