Eularian Path
7 Bridges of Konigsburg
An Eulerian Path, named after mathematician Leonhard Euler, is a traveral of a graph that visits each edge exactly once.
The famous 7 Bridges of Konigsberg problem, first solved by Euler, gave rise to the idea of an Eulerian Path, and was the foundation of modern graph theory.
The city of Konigsberg contained 7 bridges. Citizens would attempt to walk around the city while traversing the bridges only once.
Below is a simplified version of Koningsberg
In order to solve the the 7 Bridges of Konigsberg problem, we’ll need to make a few observations.
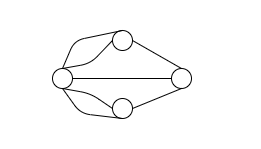
Let’s examine the following picture:
Suppose we’ve started our traversal of the graph on a different node than Node 1 (shown in Picture 2).
If we want to traverse every edge, then we will have to use 1 edge to get to Node 1, 1 edge to leave Node 1, and another edge to get back to Node 1.
However, once we are back at Node 1, we are stuck.
We have a couple ways we could fix the situation.
- We can add or remove edges from Node 1 so that Node 1 has an even degree; we need each incoming edge to Node 1 to have a corresponding outgoing edge so that we don’t get stuck.
- We could start our traversal from Node 1. This way, we can leave Node 1, come back to Node 1, and leave again with no problem.
- Similarly, we could end our traversal at Node 1. This way, we can visit Node 1, leave, then come back again.
This gives us an idea of how to approach the 7 Bridges problem.
Notice that a node that is not the starting point or the ending point must have an even degree.
The starting point and the ending point are the only 2 nodes allowed to have an odd degree.
Thus, in order for an Eulerian path to exist, there must be either 0 or 2 nodes with an odd degree.
In addition, the graph must be a connected graph - otherwise, we may not be able to reach some edges.
Let’s go back to the 7 Bridges of Koningsberg, and apply our idea.
Note that all 4 nodes have a degree of 3. Thus, there is no Eularian path.
Algorithm for Eularian Paths
Although our observations above identify if there exists an Eulerian path, it does not tell us what the actual Eularian path is.
There are 2 algorithms used to find an Eularian path.
####### Fleury’s algorithm for Eularian Paths:
For Fleury’s algorithm, we need to find out if there are any nodes with odd degrees. If there are, we will choose the starting node as one of them.
Otherwise, we will pick an arbitrary edge.
For each iteration, we will run Tarjan’s Algorithm for Bridges to locate the bridges in the graph. A bridge is an edge that, if removed, will cause the graph to become disconnected.
Afterwards, we pick a random edge attached to our current node. We cannot pick any bridges, as this would mean we would be unable to traverse between parts of the graph.
The only case in which we pick a bridge is if we don’t have a choice.
We repeat the process until all edges have been traversed.
The proof of correctness is somewhat complicated, so we won’t discuss it here.
Hierholzer’s algorithm for Eularian Cycles:
An Eularian cycle is an Eularian path that ends at the starting point. For an Eulerian cycle to exist, there cannot be any nodes with odd degree.
Try to convince yourself why after looking at Heirholzer’s algorithm.
Hierholzer’s algorithm starts at any arbitrary node. Then, we traverse the graph by randomly picking edges and deleting them. The only node that we can get stuck on is the starting node, since it has an odd degree.
Once we get back to the starting node, we have 2 cases:
- All the edges have been traversed. In this case, we are done.
- Not all the edges have been traversed. In this case, we can pick a random node on the path we just traversed that still has degree > 0. We use this node as our new starting point and continue to traverse the graph by picking random edges. The only way we can get stuck is by traversing back to our new starting point (same logic as above). We can then take the path we just traversed and attach it to our original one. We repeat the process until we have traversed all the edges.